Sketch Elements

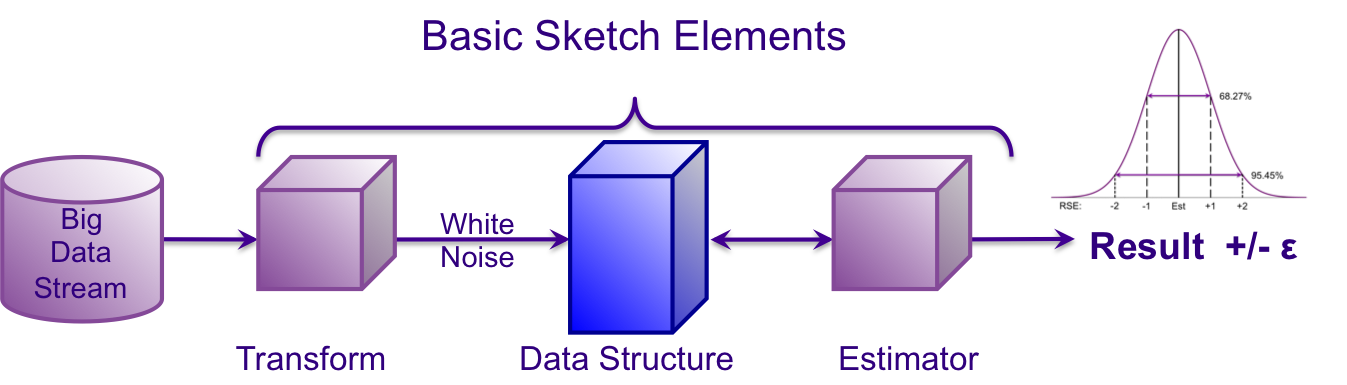
Sketches are different from traditional sampling techniques in that sketches examine all the elements of a stream, touching each element only once, and often have some form of randomization that forms the basis of their stochastic nature. This “one-touch” property makes sketches ideally suited for real-time stream processing.

As an example, the first stage of a count-distinct sketching process is a transformation that gives the input data stream the property of white noise, or equivalently, a uniform distribution of values. This is commonly achieved by coordinated hashing of the input unique keys and then normalizing the result to be a uniform random number between zero and one.

The second stage of the sketch is a data structure that follows a set of rules for retaining a small set of the hash values it receives from the transform stage. Sketches also differ from simple sampling schemes in that the size of the sketch often has a configurable, fixed upper bound, which enables straightforward memory management.

The final element of the sketch process is a set of estimator algorithms that upon a request examine the sketch data structure and return a result value. This result value will be approximate but will have well established and mathematically proven error distribution bounds.

Sketches are typically¹

• Small in size. They are typically orders of magnitude smaller than the raw input data stream. Sketches implement sublinear algorithms that grow in size much slower than that of the size of the input stream. Some sketches have a finite upper-bound in size that is independent of the size of the input stream.
• Fast. The update times are independent of the size or order of the input stream. These sketches are inherently “Single Pass” or “One Touch”. The sketch only needs to see each item in the stream once.
• Highly Parallelizable. The sketch data structures are “additive” in that they can be merged without losing accuracy.
• Approximate. As an example, for unique count sketches the relative error bounds are a function of the configured size of the sketch.

¹ For a more comprehensive definition see Sketch Criteria