Contents

• Introduction to the Quantile Sketches
• Kll Sketch
  • Comparing the KllSketches with the original classic Quantiles Sketches
  • Plots for KllDoublesSketch vs. classic Quantiles DoublesSketch
  • Simple Java KLL Example
• KLL Accuracy And Size
• Understanding KLL Bounds
• Examples
  • KLL Sketch C++ Example
• Tutorials
  • Sketching Quantiles and Ranks Tutorial
• Theory
  • Optimal Quantile Approximation in Streams
  • References

KLL Sketch

This is an implementation of a very compact quantiles sketch with lazy compaction scheme and nearly optimal accuracy per bit of storage. The underlying theoretical work is the paper Optimal Quantile Approximation in Streams, by Zohar Karnin, Kevin Lang, Edo Liberty. The name KLL is composed of the initial letters of the last names of the authors.

This implementation includes 16 variations of the KLL Sketch, including a base KllSketch for methods common to all sketches. The implementation variations are across 3 different dimensions:

• Input type: double, float, long, item(generic)
• Memory type: heap, direct (off-heap)
• Stored Size: compact (read-only), updatable

With the one exception that the KllItemSketch is not available in direct, updatable form. The classes are organized in an inheritance hierarchy as follows:

• Public KllSketch
  • Public KllDoublesSketch
    • KllHeapDoublesSketch
    • KllDirectDoublesSketch
      • KllDirectCompactDoublesSketch
  • Public KllFloatsSketch
    • KllHeapFloatsSketch
    • KllDirectFloatsSketch
      • KllDirectCompactFloatsSketch
  • Public KllItemsSketch
    • KllHeapItemsSketch
    • KllDirectCompactItemsSketch
  • Public KllLongsSketch
    • KllHeapLongsSketch
    • KllDirectLongsSketch
      • KllDirectCompactLongsSketch

The internal package-private variations are constructed using static factory methods from the 4 outer public classes for doubles, floats, items, and longs, respectively

Comparing the KLL Sketches with the original classic Quantiles Sketches

The usage of KllDoublesSketch is very similar to the classic quantiles DoublesSketch.

• The key feature of KLL sketch is its compactness for a given accuracy. KLL has a much smaller size for the same accuracy (see the plots below).
• The KLL parameter K, which affects accuracy and size, doesn’t have to be power of 2. The default K of 200 was chosen to yield approximately the same normalized rank error (1.65%) as the classic quantiles DoublesSketch (K=128, error 1.73%).
• The classic quantiles sketch only has double and item(generic) input types, while KLL (as mentioned above) is implemented with double, float, long, and item(generic) types.
• KLL uses a merge method rather than a union object.

Plot Comparisons of KllDoublesSketch vs. classic Quantiles DoublesSketch

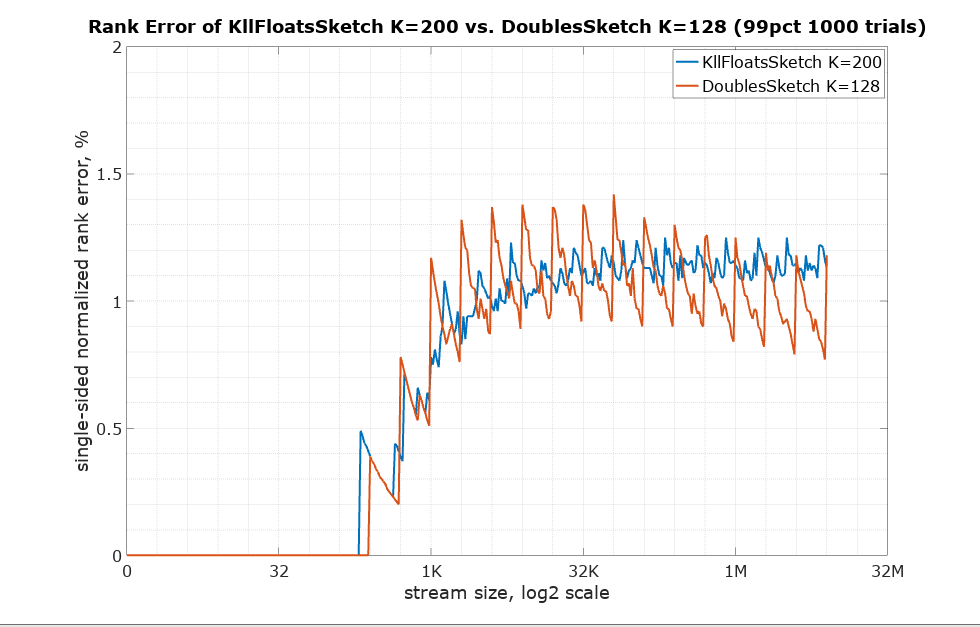
The starting point for the plot comparisons is setting K in such a way that rank error would be approximately the same. As pointed out above, the default K for both sketches should achieve this. Here is the comparison of the single-sided normalized rank error (getRank() method) for the default K:

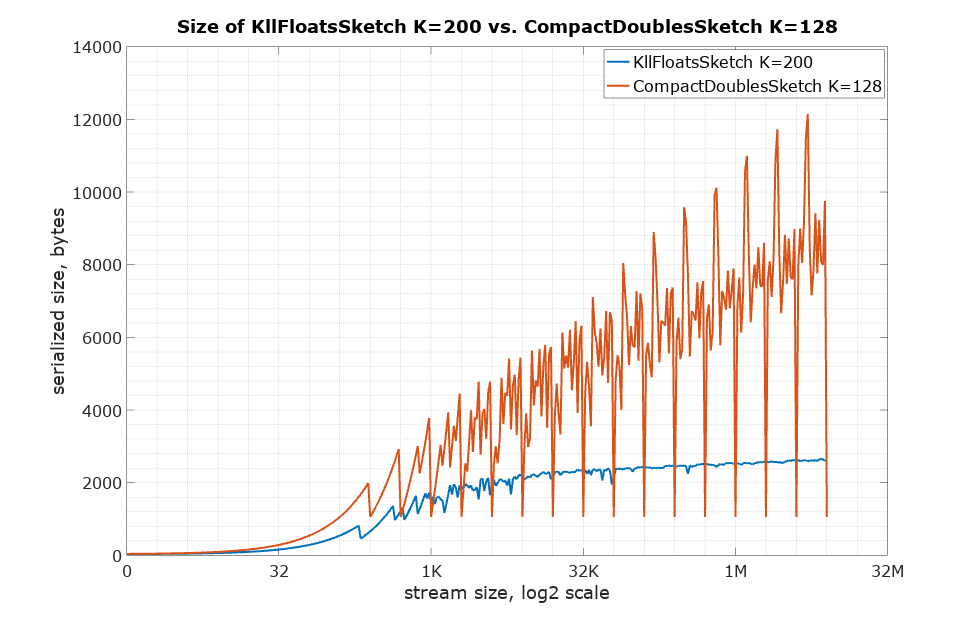
The classic quantiles DoublesSketch has two forms with different serialized sizes: UpdateDoublesSketch and CompactDoublesSketch. The KLL sketches makes this distinction differently. When the KllSketch is serialized using toByteArray() it is always in a compact form and immutable. When the KllSketch is on-heap it is always updatable. It can be created off-heap using the static factory method newDirectInstance(…) method, which is also updatable. It is possible to move from off-heap (Direct) to on-heap using the heapify(Memory) method. The merge(…) method will work with off-heap sketches, on-heap sketches and Memory wrapped compact byte arrays.

Here is the comparison of serialized sizes:

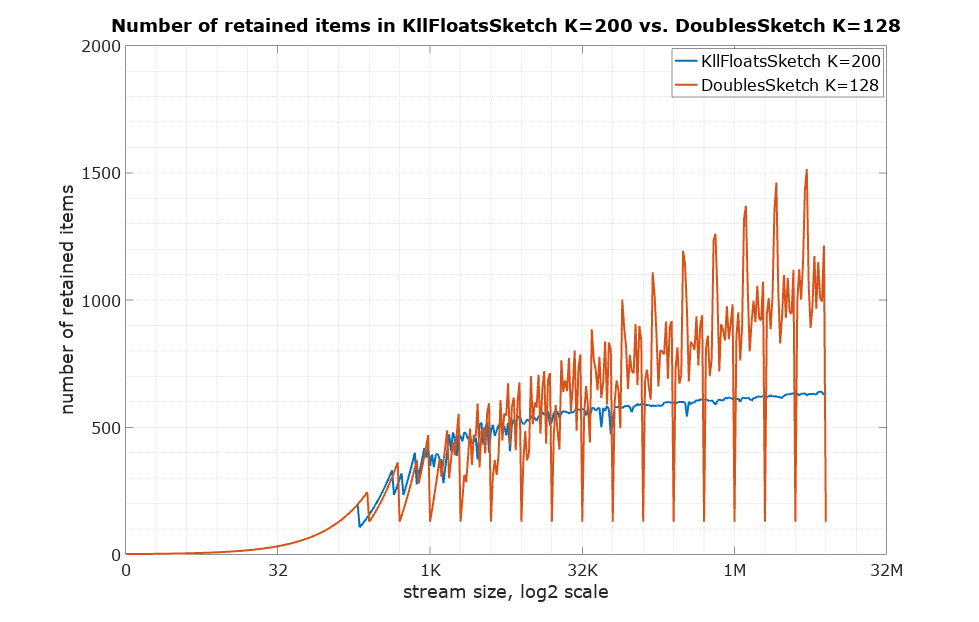
Here is the comparison of the number of retained items to see the difference with no influence of the size of the item type:

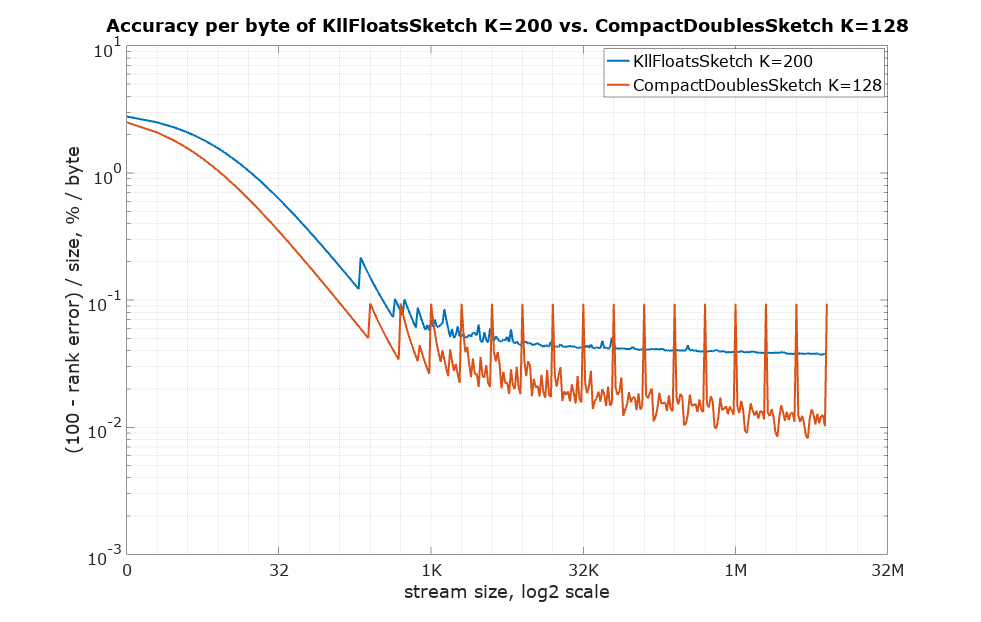
Below is the accuracy per byte measure (the higher the better). Suppose rank error is 1%, so the corresponding accuracy would be 99%. Divide that by size in bytes to arrive at this measure of how expensive each percentage point is in terms of space needed:

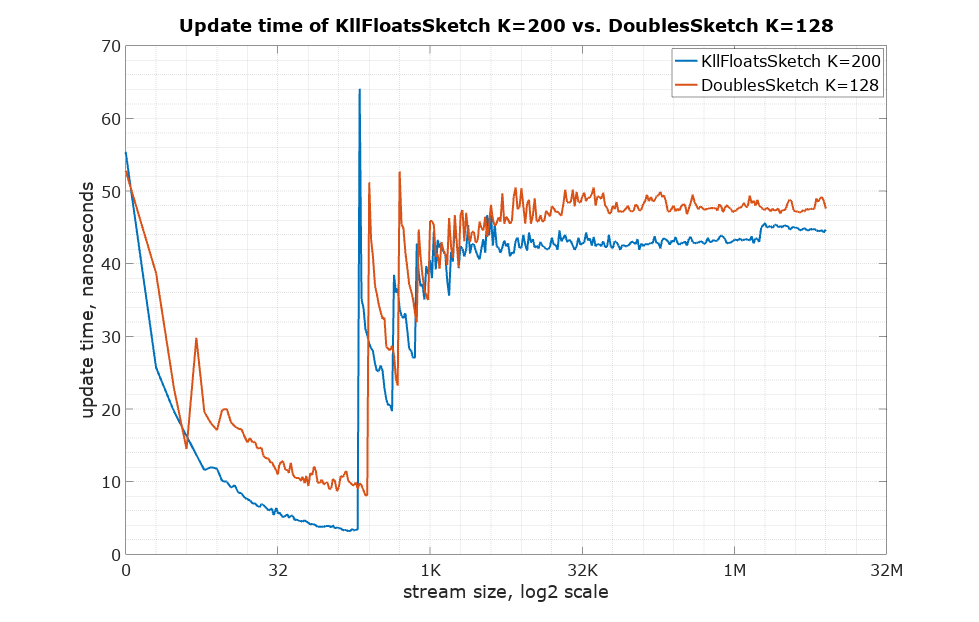
Below is the update() method speed:

Simple Java KLL Floats example

import org.apache.datasketches.kll.KllFloatsSketch;

KllFloatsSketch sketch = KllFloatsSketch.newHeapInstance();
int n = 1000000;
for (int i = 0; i < n; i++) {
  sketch.update(i);
}
float median = sketch.getQuantile(0.5);
double rankOf1000 = sketch.getRank(1000);