KLL Sketch Accuracy and Size Vs K and N

The accuracy of the KLL quantile sketch is a function of the configured K, which also affects the overall size of the sketch (default K = 200).

The accuracy of quantiles sketches is specified and measured with respect to the rank only, not the quantiles.

The KLL Sketch has absolute error. For example, a specified rank accuracy of 1% at the median (rank = 0.50) means that the true quantile (if you could extract it from the set) should be between getQuantile(0.49) and getQuantile(0.51). This same 1% error applied at a rank of 0.95 means that the true quantile should be between getQuantile(0.94) and getQuantile(0.96). In other words, the error is a fixed +/- epsilon for the entire range of ranks.

The approximate rank error values listed in the second row of the header in the table below can be computed using the function KLLSketch.getNormalizedRankError(int k, false). The third row shows the double-sided error that applies to a portion of the distribution such as an element of PMF (bar in a histogram) that is a subject to rank error on both sides. It can be computed using the function KLLSketch.getNormalizedRankError(int k, true).

KllFloatsSketch (Java) or kll_sketch<float> (C++) serialized size in bytes from K or rank error % vs. N.

N K=25 K=50 K=100 K=200 K=400 K=800 K=1600
single-sided error 10.04% 5.12% 2.61% 1.33% 0.68% 0.35% 0.18%
double-sided error 11.74% 6.11% 3.18% 1.65% 0.86% 0.45% 0.23%
0 8 8 8 8 8 8 8
1 40 40 40 40 40 40 40
2 44 44 44 44 44 44 44
4 52 52 52 52 52 52 52
8 68 68 68 68 68 68 68
16 100 100 100 100 100 100 100
32 120 164 164 164 164 164 164
64 188 196 292 292 292 292 292
128 220 336 352 548 548 548 548
256 268 396 632 664 1,060 1,060 1,060
512 288 524 744 1,224 1,288 2,084 2,084
1,024 356 568 988 1,436 2,404 2,536 4,132
2,048 392 556 1,036 1,912 2,812 4,768 5,032
4,096 428 628 1,012 1,996 3,740 5,580 9,492
8,192 448 656 1,004 2,156 3,844 7,440 11,116
16,384 496 708 1,224 2,148 4,104 7,648 14,820
32,768 528 740 1,260 2,344 4,384 8,236 15,228
65,536 556 764 1,292 2,120 4,664 8,772 16,236
131,072 612 800 1,304 2,436 4,740 9,280 17,592
262,144 632 844 1,352 2,464 4,744 8,644 18,268
524,288 680 880 1,392 2,512 4,780 9,344 18,724
1,048,576 720 916 1,436 2,548 4,772 9,560 18,932
2,097,152 744 948 1,460 2,584 4,860 9,584 19,008
4,194,304 780 1,000 1,500 2,616 4,928 9,572 18,892
8,388,608 812 1,032 1,540 2,640 4,960 9,656 19,036
16,777,216 852 1,052 1,584 2,680 5,000 9,708 19,204
33,554,432 892 1,108 1,620 2,724 5,032 9,728 18,620
67,108,864 928 1,124 1,648 2,760 5,040 9,764 19,276
134,217,728 936 1,168 1,688 2,780 5,100 9,808 19,304
268,435,456 964 1,200 1,696 2,832 5,136 9,848 19,336
536,870,912 992 1,232 1,752 2,868 5,176 9,876 19,396
1,073,741,824 1,020 1,284 1,784 2,888 5,212 9,924 19,404
2,147,483,648 1,080 1,308 1,824 2,924 5,244 9,956 19,448
4,294,967,296 1,108 1,356 1,864 2,976 5,264 9,980 19,488
8,589,934,592 1,148 1,384 1,888 2,992 5,312 10,032 19,540
17,179,869,184 1,188 1,432 1,936 3,040 5,344 10,052 19,576

KllDoublesSketch (Java) or kll_sketch<double> (C++) serialized size in bytes from K or rank error % vs. N.

N K=25 K=50 K=100 K=200 K=400 K=800 k=1600
single-sided error 10.04% 5.12% 2.61% 1.33% 0.68% 0.35% 0.18%
double-sided error 11.74% 6.11% 3.18% 1.65% 0.86% 0.45% 0.23%
0 8 8 8 8 8 8 8
1 56 56 56 56 56 56 56
2 64 64 64 64 64 64 64
4 80 80 80 80 80 80 80
8 112 112 112 112 112 112 112
16 176 176 176 176 176 176 176
32 212 304 304 304 304 304 304
64 348 364 560 560 560 560 560
128 408 644 676 1,072 1,072 1,072 1,072
256 500 760 1,236 1,300 2,096 2,096 2,096
512 536 1,012 1,456 2,420 2,548 4,144 4,144
1,024 668 1,096 1,940 2,840 4,780 5,044 8,240
2,048 736 1,068 2,032 3,788 5,592 9,508 10,036
4,096 804 1,208 1,980 3,952 7,444 11,128 18,956
8,192 840 1,260 1,960 4,268 7,648 14,844 22,200
16,384 932 1,360 2,396 4,248 8,164 15,256 29,604
32,768 992 1,420 2,464 4,636 8,720 16,428 30,416
65,536 1,044 1,464 2,524 4,184 9,276 17,496 32,428
131,072 1,152 1,532 2,544 4,812 9,424 18,508 35,136
262,144 1,188 1,616 2,636 4,864 9,428 17,232 36,484
524,288 1,280 1,684 2,712 4,956 9,496 18,628 37,392
1,048,576 1,356 1,752 2,796 5,024 9,476 19,056 37,804
2,097,152 1,400 1,812 2,840 5,092 9,648 19,100 37,952
4,194,304 1,468 1,912 2,916 5,152 9,780 19,072 37,716
8,388,608 1,528 1,972 2,992 5,196 9,840 19,236 38,000
16,777,216 1,604 2,008 3,076 5,272 9,916 19,336 38,332
33,554,432 1,680 2,116 3,144 5,356 9,976 19,372 37,160
67,108,864 1,748 2,144 3,196 5,424 9,988 19,440 38,468
134,217,728 1,764 2,228 3,272 5,460 10,104 19,524 38,520
268,435,456 1,816 2,288 3,284 5,560 10,172 19,600 38,580
536,870,912 1,868 2,348 3,392 5,628 10,248 19,652 38,696
1,073,741,824 1,920 2,448 3,452 5,664 10,316 19,744 38,708
2,147,483,648 2,036 2,492 3,528 5,732 10,376 19,804 38,792
4,294,967,296 2,088 2,584 3,604 5,832 10,412 19,848 38,868
8,589,934,592 2,164 2,636 3,648 5,860 10,504 19,948 38,968
17,179,869,184 2,240 2,728 3,740 5,952 10,564 19,984 39,036

KLL Sketch Typical Growth Path: Size vs N

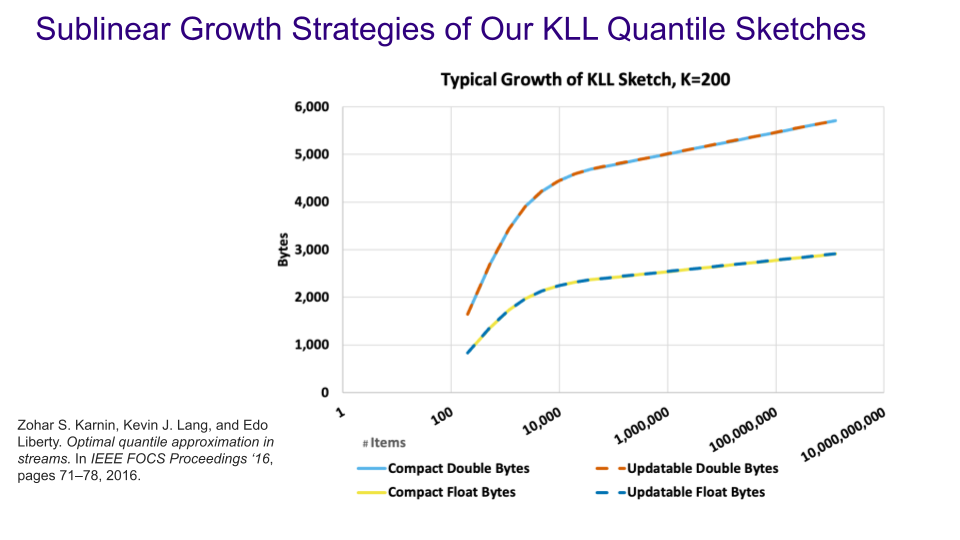
The following graph illustrates the typical size of KLL Floats and KLL Doubles Sketches vs number of items. Once the sketch, of a given K, reaches its “full compaction shape” its size grows very, very slowly. As you can see here, a KllDoubles sketch of 10^10 items would be about 6KB in size. The KllFloats sketch is about half that. This means for practical stream sizes, the KLL sketches stay pretty small.

KllGrowthPath_Floats&Doubles.png

The growth path for KLL can be estimated from equations and plots that predict the size of the sketch fairly accurately. The following plot shows the growth path normalized per byte of item size. This can be used even for items of variable size as long as you can estimate the average item size.

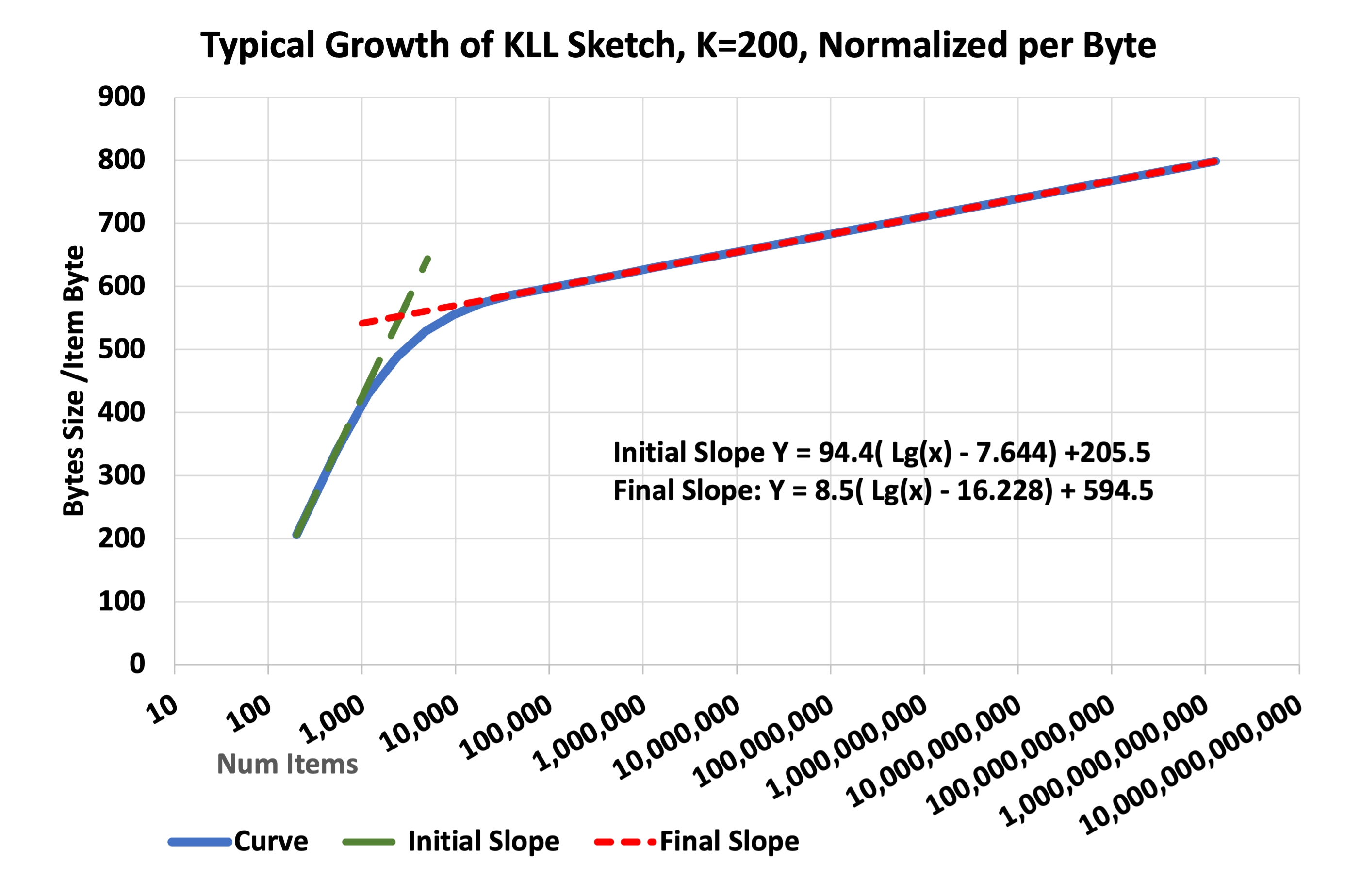
NormalizedGrowth_1B_K200.png

A KLL sketch of a larger”K”, would shift this graph to the right. A smaller “K” would shift it to the left.