Please review the Quantiles Tutorial.
The accuracy of a quantile sketch is a function of the configured value k, which also affects the overall size of the sketch.
Accuracy for quantiles sketches is specified and measured with respect to the rank only, not the values.
The Quantiles/DoublesSketch and the KLL Sketch have absolute error. For example, a specified accuracy of 1% at the median (rank = 0.50) means that the true value (if you could extract it from the set) should be between getQuantile(0.49) and getQuantile(0.51). This same 1% error applied at a rank of 0.95 means that the true value should be between getQuantile(0.94) and getQuantile(0.96). In other words, the error is a fixed +/- epsilon for the entire range of rank values.
The ReqSketch, however, has relative rank error and the user can choose which end of the rank domain should have high accuracy. Refer to the sketch documentation for more information.
A sketch is an implementation of a streaming algorithm. By definition, a sketch has only one chance to examine each item of the stream. It is this property that makes a sketch a streaming algorithm and useful for real-time analysis of very large streams that may be impractical to actually store.
We also assume that the sketch knows nothing about the input data stream: its length, the range of the values or how the values are distributed. If the authors of a particular algorithm require the user to know any of the above attributes of the input data stream in order to “tune” the algorithm, the algorithm is not data independent.
The only thing the user needs to know is how to extract the values from the stream so that they can be fed into the sketch. It is reasonable that the user knows the type of values in the stream: e.g., are they alphanumeric strings, numeric strings, or numeric primitives. These properties may determine the type of sketch to use as well as how to extract the appropriate quantities to feed into the sketch.
A k of 256 produces a normalized rank error of less than 1%. For example, the median value returned from getQuantile(0.5) will be between the actual values from the hypothetically sorted array of input values at normalized ranks of 0.49 and 0.51, with a confidence of about 99%.
The approximate error (epsilon) values listed in the second row of the header in the table below can be computed using the function double DoubleSketch.getNormalizedRankError(int k). The values in this table match very closely with empirical measurements up to k = 1024 at the 99% confidence level. Beyond k = 1024, the estimated error is somewhat speculative, but should be reasonable guidance. These error values simultaneously apply to all half-open intervals (-Infinity, Q] and closed intervals [Q1, Q2].
Table Guide for Quantiles DoublesSketch Size in Bytes and Approximate Error:
K => | 16 32 64 128 256 512 1,024 2,048 4,096 8,192 16,384 32,768
~ Error => | 12.145% 6.359% 3.317% 1.725% 0.894% 0.463% 0.239% 0.123% 0.063% 0.033% 0.017% 0.009%
N | Size in Bytes ->
----------------------------------------------------------------------------------------------------------------------------------------
0 | 8 8 8 8 8 8 8 8 8 8 8 8
1 | 64 64 64 64 64 64 64 64 64 64 64 64
3 | 64 64 64 64 64 64 64 64 64 64 64 64
7 | 96 96 96 96 96 96 96 96 96 96 96 96
15 | 160 160 160 160 160 160 160 160 160 160 160 160
31 | 288 288 288 288 288 288 288 288 288 288 288 288
63 | 416 544 544 544 544 544 544 544 544 544 544 544
127 | 544 800 1,056 1,056 1,056 1,056 1,056 1,056 1,056 1,056 1,056 1,056
255 | 672 1,056 1,568 2,080 2,080 2,080 2,080 2,080 2,080 2,080 2,080 2,080
511 | 800 1,312 2,080 3,104 4,128 4,128 4,128 4,128 4,128 4,128 4,128 4,128
1,023 | 928 1,568 2,592 4,128 6,176 8,224 8,224 8,224 8,224 8,224 8,224 8,224
2,047 | 1,056 1,824 3,104 5,152 8,224 12,320 16,416 16,416 16,416 16,416 16,416 16,416
4,095 | 1,184 2,080 3,616 6,176 10,272 16,416 24,608 32,800 32,800 32,800 32,800 32,800
8,191 | 1,312 2,336 4,128 7,200 12,320 20,512 32,800 49,184 65,568 65,568 65,568 65,568
16,383 | 1,440 2,592 4,640 8,224 14,368 24,608 40,992 65,568 98,336 131,104 131,104 131,104
32,767 | 1,568 2,848 5,152 9,248 16,416 28,704 49,184 81,952 131,104 196,640 262,176 262,176
65,535 | 1,696 3,104 5,664 10,272 18,464 32,800 57,376 98,336 163,872 262,176 393,248 524,320
131,071 | 1,824 3,360 6,176 11,296 20,512 36,896 65,568 114,720 196,640 327,712 524,320 786,464
262,143 | 1,952 3,616 6,688 12,320 22,560 40,992 73,760 131,104 229,408 393,248 655,392 1,048,608
524,287 | 2,080 3,872 7,200 13,344 24,608 45,088 81,952 147,488 262,176 458,784 786,464 1,310,752
1,048,575 | 2,208 4,128 7,712 14,368 26,656 49,184 90,144 163,872 294,944 524,320 917,536 1,572,896
2,097,151 | 2,336 4,384 8,224 15,392 28,704 53,280 98,336 180,256 327,712 589,856 1,048,608 1,835,040
4,194,303 | 2,464 4,640 8,736 16,416 30,752 57,376 106,528 196,640 360,480 655,392 1,179,680 2,097,184
8,388,607 | 2,592 4,896 9,248 17,440 32,800 61,472 114,720 213,024 393,248 720,928 1,310,752 2,359,328
16,777,215 | 2,720 5,152 9,760 18,464 34,848 65,568 122,912 229,408 426,016 786,464 1,441,824 2,621,472
33,554,431 | 2,848 5,408 10,272 19,488 36,896 69,664 131,104 245,792 458,784 852,000 1,572,896 2,883,616
67,108,863 | 2,976 5,664 10,784 20,512 38,944 73,760 139,296 262,176 491,552 917,536 1,703,968 3,145,760
134,217,727 | 3,104 5,920 11,296 21,536 40,992 77,856 147,488 278,560 524,320 983,072 1,835,040 3,407,904
268,435,455 | 3,232 6,176 11,808 22,560 43,040 81,952 155,680 294,944 557,088 1,048,608 1,966,112 3,670,048
536,870,911 | 3,360 6,432 12,320 23,584 45,088 86,048 163,872 311,328 589,856 1,114,144 2,097,184 3,932,192
1,073,741,823 | 3,488 6,688 12,832 24,608 47,136 90,144 172,064 327,712 622,624 1,179,680 2,228,256 4,194,336
2,147,483,647 | 3,616 6,944 13,344 25,632 49,184 94,240 180,256 344,096 655,392 1,245,216 2,359,328 4,456,480
4,294,967,295 | 3,744 7,200 13,856 26,656 51,232 98,336 188,448 360,480 688,160 1,310,752 2,490,400 4,718,624
The following graphs illustrate the ability of the Quantiles DoublesSketch to characterize value distributions.
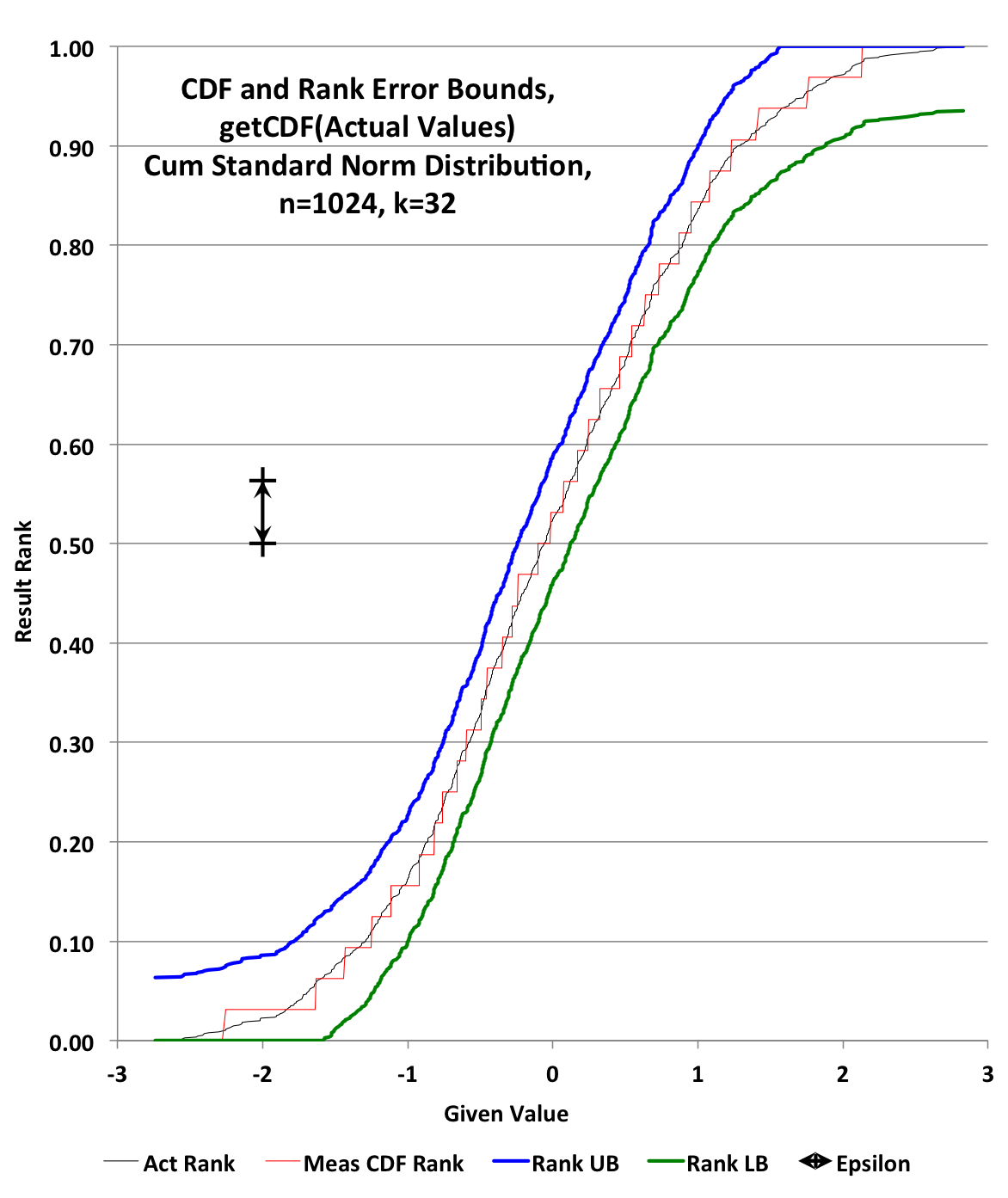
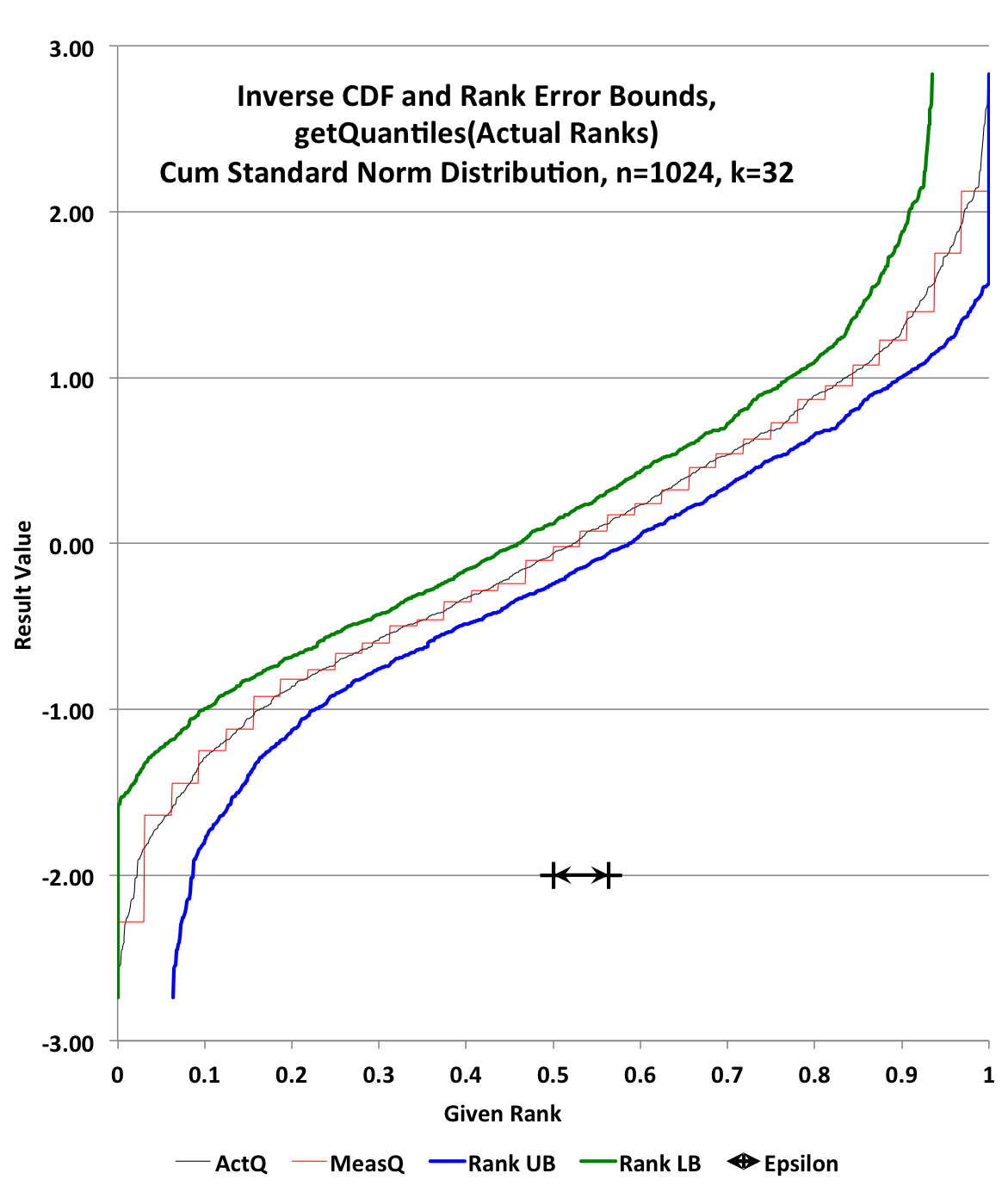
1024 (n) values (trueUnsortedValues) were generated from Random’s nextGaussian(). These values were then sorted (trueSortedValues) and assigned their true normalized ranks (trueRanks) from 0 to (n-1)/n.
A DoublesSketch (sketch) was then created with K = 32 and updated with the trueUnsortedValues.
sketch.getCDF(trueSortedValues) produced an ordered array of estimated ranks (estimatedRanks) . The estimatedRanks (red) were then plotted against the trueRanks (black). The upper bound error was plotted in blue and the lower bound error was plotted in green.
The error of the estimation from the sketch is called “Epsilon” and is always with respect to the rank axis. It was plotted as a visual bar on the graph to illustrate its size.
The size of this sketch, if stored, would be about 1832 bytes.
The absolute rank error vs the trueRanks produced the following graph.
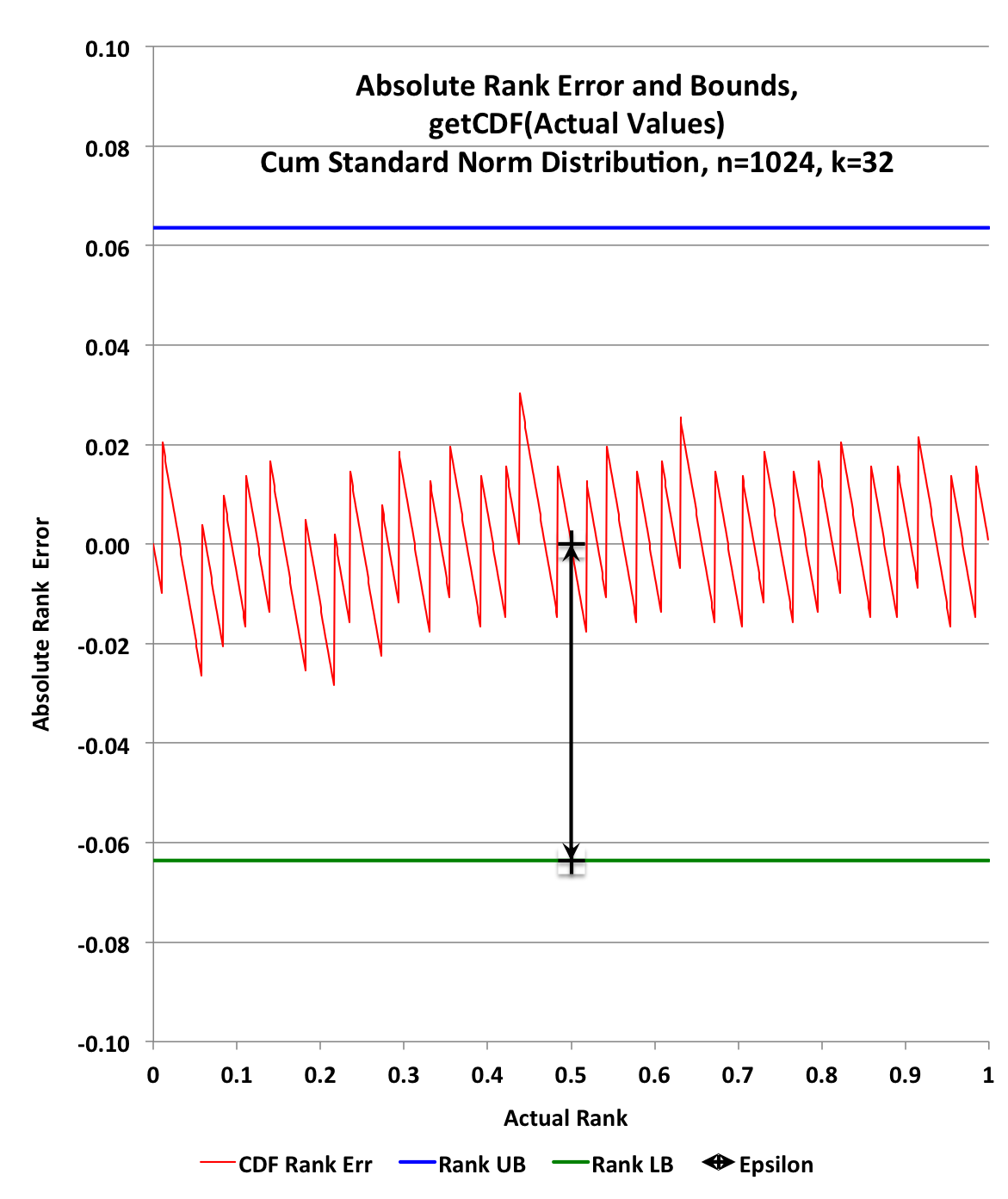
All of the above plots were generated from one trial, and is not a test of the error bounds.
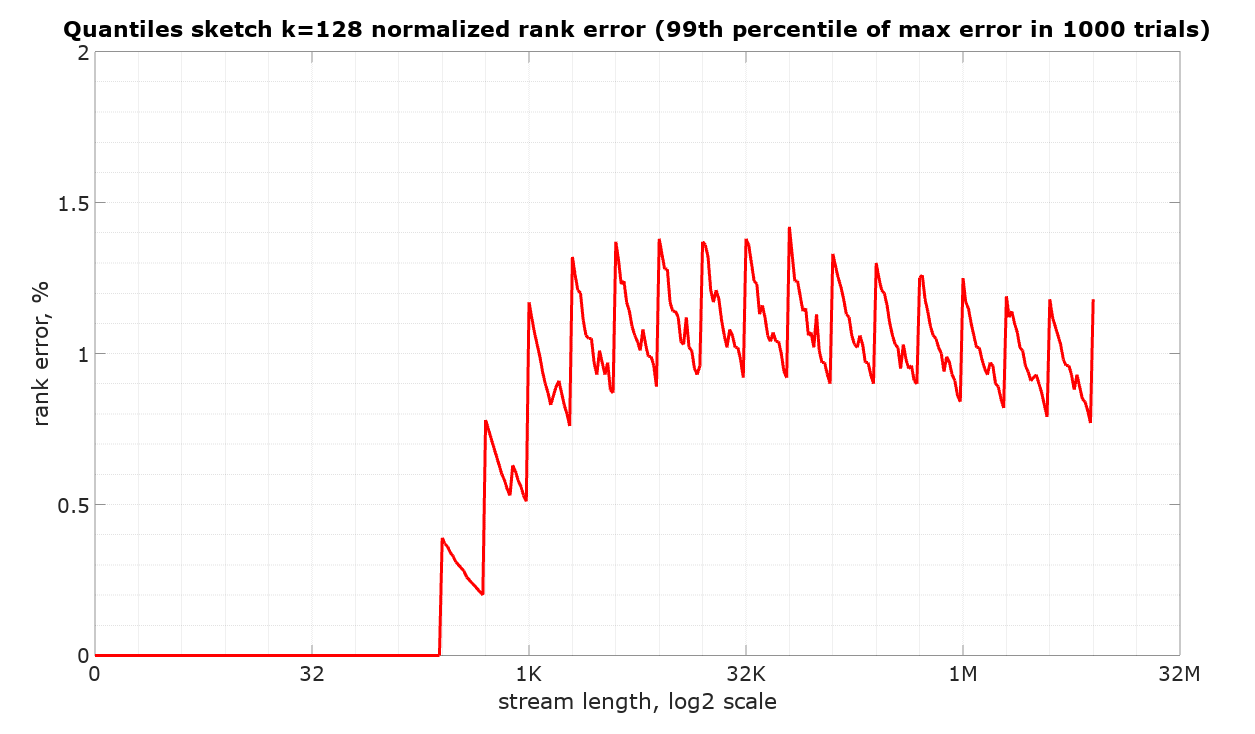
The following plot illustrates the 99th percentile of observed maximum normalized rank error of DoublesSketch with k=128 in 1000 trials at each stream length. The code to reproduce this measurement is available in the DataSketches/characterization repository. Note that these measurements are not directly comparable to the values in the table above as this graph plots the error for only the half-open intervals (-Infinity, Q], which is relevant to simple queries such as getRank(value).