Now lets choose k = 3, which means that we will keep the 3 smallest hash values that the cache has seen. The fractional distance that these k values consume is simply the value of the kth hash value, or V(kth), which in this example is 0.195. This is also known as the kth Minimum Value or KMV. Since these measurements are relative to zero, a sketch constructed like this is also known as a Bottom-k sketch. (It could well have been a Top-k sketch, but referencing to zero is just simpler.)
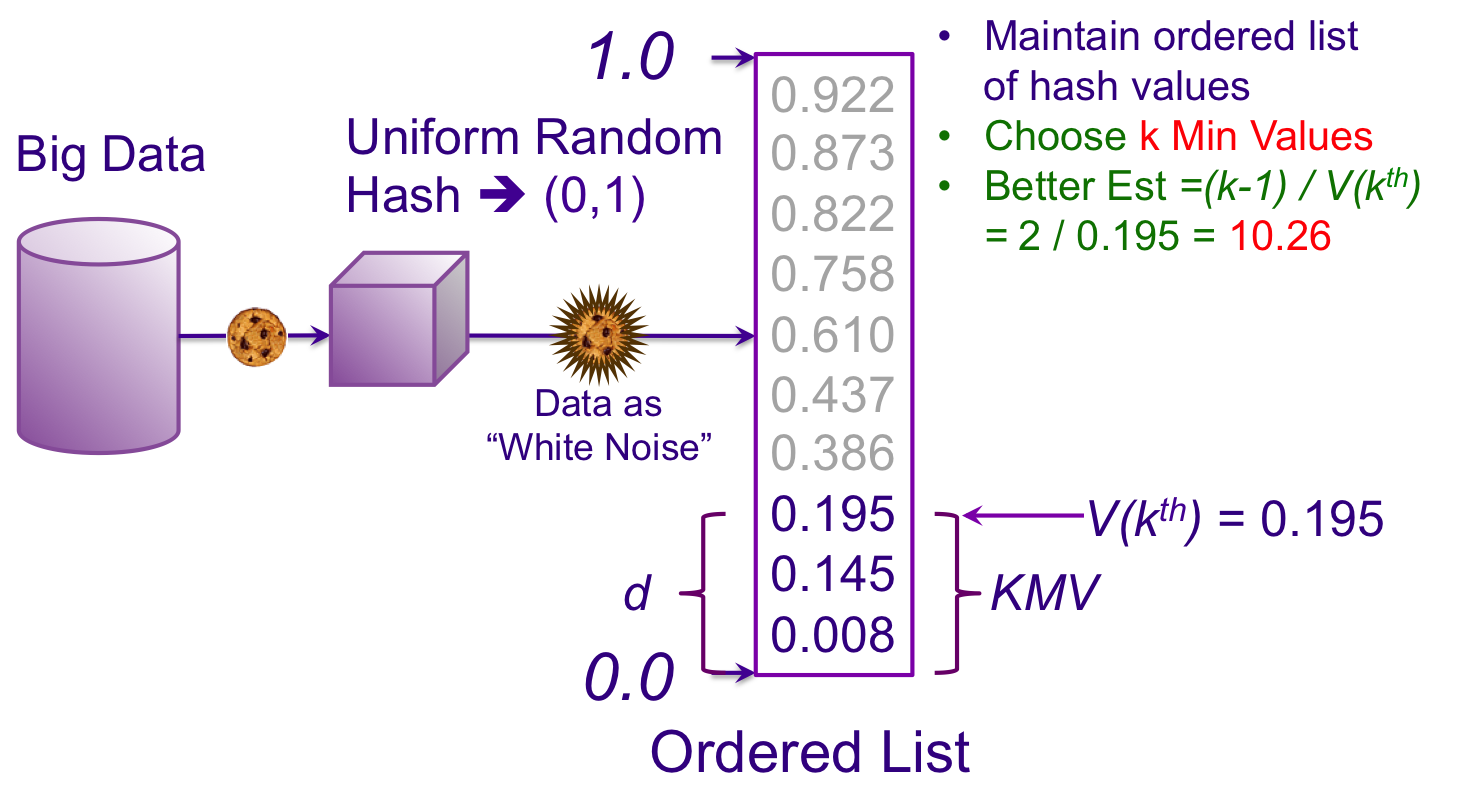
We want not only a more accurate estimate, but one that is also unbiased. I’m going to skip a few pages of calculus[1] and reveal that we only need to subtract one in the numerator to achieve that. Our new, unbiased KMV estimator becomes

This is much closer to 10, but with such a small sample size we were also lucky.
Note that with our new estimator based on the k minimum values in the cache we don’t have to keep any hash values larger than V(kth). And, since k is a constant our cache will have a fixed upper bound size independent of how many hash values it has seen.
[1] For those interested in the mathematical proofs, Giroire has a straightforward and easy-to-follow development.